0810

몸 상태 이슈로 오늘은 짧은 공부만 하고 갑니다.....

"정렬"이라는 글자만 계속 보니까 게슈탈트 붕괴옴
비서 문제가 떠오르는 오늘임

CS

정렬 알고리즘

왜 필요한데?

1. 효율적인 탐색을 위해서

탐색 안 하고 찾으면 어떻게 되는데?
- 효율적인 탐색(예컨데 이진탐색)을 하기 위해선 정렬이 되어있어야 됨
- 정렬이 되어있지 않아도 선형 탐색을 활용해 데이터를 찾을 수는 있지만 O(n)의 시간 복잡도가 걸림.
- 반면 정렬된 데이터로 이진 탐색을 할 경우 O(log n)의 시간복잡도가 걸림.

2. 중복 제거를 위해서

정렬하면 같은 값들이 연속해서 모이니까, 순회를 한 번만 해서 앞 원소랑 비교 후 중복을 쉽게 걸러낼 수 있음. 정렬을 통한 중복 제거는 자료구조 제약 없이 가능함.
hashset 자료형을 쓸 수 없을 때 정렬 기반 중복 제거를 씀. 정렬 기반 중복 제거는 메모리 사용량이 적지만 정렬 비용이 발생하고, hashset은 메모리가 많이 사용됨.

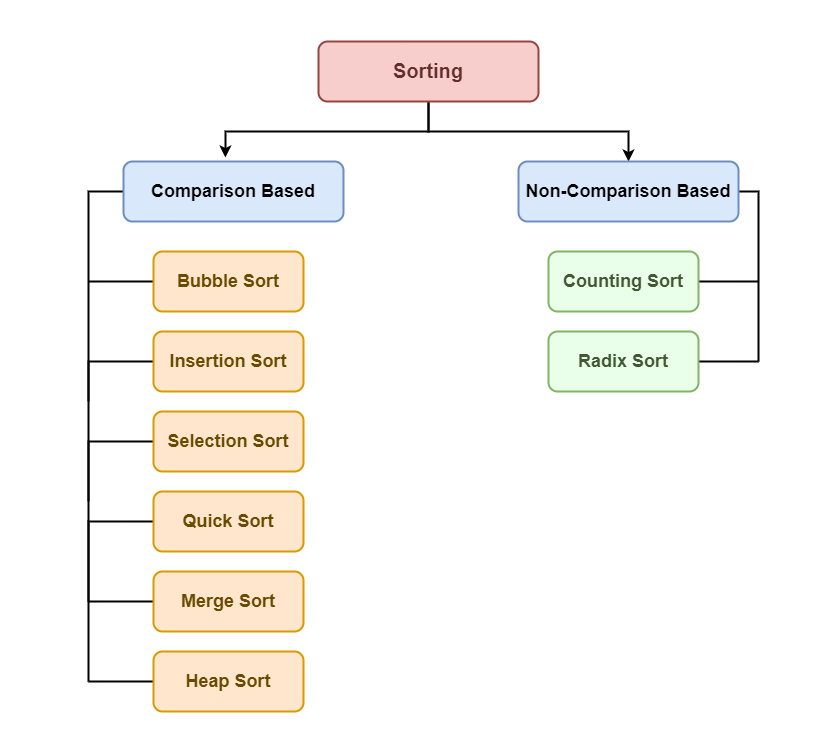
Pasted image 20250810115401

comparison based VS non-comparsion

comparison based는 요소를 비교하여 순서를 결정하는 반면
non-comparsion은 직접적인 요소 비교 없이 순서를 결정하는 것

1. 비교 기반 (Comparison-based)

단순(비효율) 정렬
- 버블 정렬 (Bubble Sort): O(n²)
  - 인접한 두 원소를 비교하여 뒤(또는 앞)로 보내는 방식. 거품처럼 밀려나서 버블 정렬
- 삽입 정렬 (Insertion Sort): O(n²)
  - 이미 정렬된 부분에 새로운 원소를 알맞은 위치에 삽입하는 방식.
  - 왼쪽 구간(이미 정렬된 부분)이 항상 정렬되어 있도록 유지한다는거임.
  - 걍 보통 인간한테 이것 좀 정렬해봐 하면 웬만해서 삽입 정렬 알고리즘 쓸 듯 아닌가
  - https://www.quora.com/What-are-the-real-world-examples-for-sorting-Algorithms => 어떤 정렬 알고리즘이 젤 조을까요 => 상황마다 다르다
- 선택 정렬 (Selection Sort): O(n²)
  - 남은 원소 중 최소값(또는 최대값)을 찾아 맨 앞(또는 뒤)과 교환하는 방식.
  - 매 단계마다 가장 작은/큰 값을 뽑아서 정렬하는거임.
효율 정렬
- 퀵 정렬 (Quick Sort): 평균 O(n log n), 최악 O(n²)
  - pivot(중심점)을 선택해서 pivot보다 작은 값과 큰 값으로 분할한 뒤 재귀적으로 정렬.
- 병합 정렬 (Merge Sort): O(n log n), 안정 정렬
  - 자료를 반으로 나눠서 각각 정렬 후 병합.
- 힙 정렬 (Heap Sort): O(n log n), 불안정 정렬
  - 최대힙, 최소힙.

2. 비비교 기반 (Non-comparison-based)

계수 정렬 (Counting Sort): O(n + k) k는 값의 범위
- 각 값의 빈도를 세어 누적합을 이용해 정렬 위치를 결정.
기수 정렬 (Radix Sort): O(nk) k는 자릿수 길이
- 자릿수(1의자리, 10의 자리, 100의 자리) 또는 비트별로 정렬.
- 만약 요소의 길이가 제각각이라면 부족한 부분은 공백이나 0으로 채워서 처리함.
- LSD(Least Significant Digit first)와 MSD((Most Significant Digit first)가 있는데 LSD는 최소 자릿수부터 비교하는거고 MSD는 큰 자릿수부터 비교하는거